ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟ (بخش دوم)

این مقاله یکی از قسمت‌های سلسله مقالات یادنامه آلن تورینگ است. این مجموع پیش از این در ماهنامه شبکه منتشر شده اما به سایت جدید منتقل نشده بود. با توجه به اهمیت موضوع، این مجموعه را به سایت مجله اضافه می‌کنیم و امیدواریم که مورد توجه علاقمندان قرار بگیرد.

برای مطالعه قسمت‌ قبل ماشین تورینگ روی لینک‌های زیر کلیک کنید:

مطلب پیشنهادی

طلوع

ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟ (بخش نخست)

ماشین تورینگ

ماشین تورینگ دستگاهی است که بر‌اساس قواعدی که در یک جدول آورده شده، علامت‌های نوشته شده روی یک نوار کاغذی را خوانده و بر‌اساس توالی آن‌ها، محاسباتی را انجام می‌دهد. با وجود سادگی، این ماشین می‌تواند منطق هر الگوریتم کامپیوتری را شبیه‌سازی کرده و به طور خاص، یک مثال خوب در توضیح عملکرد پردازنده‌های مرکزی درون کامپیوترها به شمار می‌آید. 
این ماشین نخستین‌بار توسط آلن تورینگ در سال 1936 و در قالب یک مقاله، در پاسخ به مسئله‌ای که ریاضیدان آلمانی، دیوید هیلبرت منتشر کرده بود، مطرح شد. مسئله هیلبرت تصمیم‌گیری درباره این بود که آیا یک روال مشخص وجود دارد که بتواند صحت یک عبارت منطقی را در مراحلی متناهی محاسبه کند یا خیر؟ وی برای پاسخگویی به این سؤال‌، چنین ماشینی را تصور کرد و در نهایت به پاسخ منفی برای مسئله هیلبرت دست یافت. در اکتبر همان سال، فردی به نام امیل پست (Emil Post) مقاله‌ای با عنوان «Finite combinatory processes – formulation 1» منتشر کرد که در آن به توضیح و تبیین نوعی ماشین پرداخته شده بود که می‌توان آن را نوع خاصی از ماشین تورینگ به شمار آورد. کار وی مستقل از تورینگ انجام شده بود با این تفاوت که ماشین پست از الفبای باینری استفاده می‌کرد و مفاهیم حافظه ماشین وی حالت مجرد‌تری نسبت به تصورات تورینگ داشت. به همین جهت، گاهی به این چنین ماشین‌هایی پست-تورینگ  (Post-Turing Machines) نیز گفته می‌شود. بر این اساس، باید توجه داشت که ماشین تورینگ یک فناوری محاسباتی عملی به شمار نمی‌آید بلکه یک دستگاه مجازی و نظری برای نمایش یک ماشین محاسباتی است. ماشین تورینگ، مثال خوبی برای دانشمندان کامپیوتر در زمینه درک کامل محدودیت‌های محاسبات مکانیکی است. 

در اصل، ماشین تورینگ برای مدل‌سازی کامپیوتر کاربرد ندارد، بلکه هدف اصلی آن‌ مدل‌سازی خود مفهوم محاسبات است. 

تورینگ بعدها و در سال 1948 در مقاله‌ای با عنوان ساز و كار رايانش (Computing Machinery and Intelligent)، تعریف دقیق‌تری از ماشین خودکار محاسباتی خود ارائه کرد و نام آن را ماشین محاسبات منطقی گذارد. وی در این مقاله چنین می‌گوید: 
«... یک ظرفیت بی‌نهایت حافظه که به‌صورت نواری کاغذی با طول بی‌نهایت و تقسیم شده به مربع‌های مساوی که روی هر‌کدام امکان نوشتن علامت‌هایی وجود دارد. در هر لحظه، یک علامت در ماشین قرار می‌گیرد که علامت اسکن شده نامیده می‌شود. ماشین می‌تواند علامت مذکور را تغییر داده و در اصل، رفتار آن برگرفته از همان علامت است و دیگر علامت‌های موجود روی نوار نمی‌توانند تأثیری روی عملکرد ماشین بگذارند. نوار کاغذی می‌تواند به عقب و جلو حرکت کرده و این یکی از اصول اولیه کاری ماشین خواهد بود...» 

مطلب پیشنهادی

يادنامه پدر علوم کامپیوتر؛ مردی که با رمزها می‌رقصد!

ماشین تورینگ در اصل تشکیل یافته از چند عنصر اصلی است که عبارتند از: 

 نوار: که به بخش‌های کوچک مربع شکلی به نام سلول تقسیم شده و هرکدام می‌تواند حاوی یک علامت از یک الفبای محدود باشد. این نوار به طور دلخواه از سمت چپ یا راست نامتناهی بوده و توسط ماشین به راحتی جابه‌جا می‌شود. در بعضی از مدل‌ها، سمت چپ نوار با علامتی مشخص نشانه‌گذاری شده و نوار تنها به سمت راست نامتناهی در نظر گرفته می‌شود. 
 هد (Head): که برای خواندن و نوشتن علامت‌های روی نوار و انجام عملیات انتقال نوار به چپ یا راست مورد استفاده قرار می‌گیرد. در برخی مدل‌ها هد متحرک بوده و نوار ثابت است. 
 جدول متناهی دستورالعمل‌ها: که در برخی مواقع جدول عملکرد یا تابع گذار نامیده می‌شود، جدولی حاوی دستورالعمل‌هایی پنجگانه یا چهارگانه با فرمت qiaj→qi1aj1dk است که وظیفه تعیین عملکرد ماشین در برابر علامت‌های روی نوار را بر عهده دارد. متغیرهای آورده شده در عبارت بالا، نشان‌دهنده حالت جاری ماشین، علامت خوانده‌شده، میزان جابه‌جایی هد و... هستند. 
 ثبات حالت: حالت ماشین تورینگ را که از میان تعداد متناهی حالت مختلف انتخاب می‌شود، ذخیره می‌کند. همیشه یک حالت اولیه برای ماشین در زمان راه‌اندازی در این رجیستر ذخیره می‌شود. تورینگ معتقد بود که این رجیستر، جایگزین حالت ذهنی شخصی است که عملیات محاسبات را به انجام می‌رساند.  توجه کنید که هر جزء ماشین، یعنی حالت‌ها و علامت‌ها و همچنین هر عملکرد ماشین یعنی چاپ، پاک‌کردن و حرکت دادن نوار متناهی، گسسته و قابل جداسازی بوده و میزان حافظه در دسترس آن یعنی نوار کاملاً نامتناهی است.  یکی از مواردی که امکان دارد پیچیدگی خاصی در بر داشته باشد، state یا حالت ماشین است که می‌توان دو برداشت مختلف از آن داشت. بسیاری از افرادی که پس از تورینگ به مباحثه درباره ماشین وی پرداخته‌اند از عبارت حالت برای اشاره به نام یا مشخص‌کردن دستورالعملی که باید اجرا شود (مانند محتویات رجیستر حالت) استفاده کرده‌اند اما تورینگ در سال 1936 یک تفاوت کاملاً آشکار میان رکوردهای پیکربندی یا حالات درونی ماشین با حالت پیشرفت آن در روال محاسبات قائل بود و به همین دلیل، فرمول حالت وی حاوی دستورالعمل جاری به همراه کلیه علامت‌های روی نوار در نظر گرفته شده بود. 
بعدها و در سال 1979، مفهوم ماشین تورینگ توسط هاپ کرافت (Hopcroft) و اولمن بر‌اساس پیشرفت‌های حاصل شده، به طور کاملاً مناسب و به‌صورت هفت گانه و بر اساس <M=<Q,Γ,b,Σ,δ,q0,F فرمول‌بندی و منظم شد که در آن متغیرهای مورد استفاده به ترتیب نشان از مجموعه حالات سیستم (Q)، الفبای استفاده شده روی نوار(Γ)، علامت نشانگر فضای خالی(b)، مجموعه علامات ورودی (Σ)، جدول ‌گذار حالت‌ها(δ)، حالت اولیه (q0 ) و حالت‌های نهایی قابل قبول (F ) دارند. هر چیزی که با این مفهوم قابل توصیف باشد، یک ماشین تورینگ به شمار می‌آید.  مثالی در این زمینه، ماشین Busy Beaver معروف است که برای رسیدن به بیشینه درگیری عملیاتی در میان ماشین‌های تورینگ موجود در یک کلاس مشخص مطرح شده و مورد استفاده قرار می‌گیرد. توصیف این ماشین بر اساس مدل‌سازی مطرح شده در بالا چنین خواهد بود:

{Q = { A, B, C, HALT 
{Γ = { 0, 1 
«تهی»=b=o
{Σ = {1 
جدول 1= δ  
حالت اولیه = q0 = A  
مجموعه حالت تک عضوی {F = {HALT

مطلب پیشنهادی

يادنامه آلن تورينگ

در ذهن پدر هوش مصنوعی جهان آلن تورینگ چه می‌گذشت؟

ماشین‌های تورینگ مجازی

در کنار انواع نمونه‌های سخت‌افزاری ساخته شده، پیاده‌سازی‌های رایانه‌ای مختلفی از ماشین تورینگ وجود دارد که با سر زدن و مشاهده روند کاری‌ آن‌ها، می‌توانید به خوبی با نحوه کار ماشین تورینگ آشنا شوید. یکی از این ماشین‌های شبیه‌سازی شده که اتفاقاً ساده‌ترین و معمولی‌ترین آن‌ها نیز به شمار می‌آید در آدرس www.turing.org.uk/turing/scrapbook/tmjava.html وجود دارد و از طریق یک مرورگر معمولی قابل دسترسی است. در این ماشین، می‌توانید عملیات مربوطه را انتخاب کرده و با زدن Load داده‌های مربوطه را روی نوار نوشته و سپس با زدن Run نتیجه اجرای عملیات روی نوار مذکور را ببینید. (شکل1)

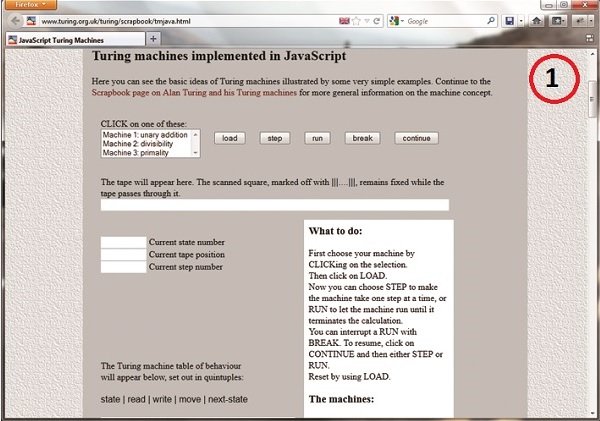
مثال قبل، نمونه چندان خوبی برای درک شهودی عملکرد ماشین تورینگ نیست چرا که عملیات خود را به یکباره و سریع انجام می‌دهد. 
در نقطه مقابل، نمونه پیاده‌سازی شده در آدرس http://ironphoenix.org/tril/tm/   عملکرد بصری مناسبی داشته و با رعایت انجام با فاصله عملیات، درک بهتری از کارکرد ماشین تورینگ با برنامه های مختلف را ارائه می‌کند. (شکل2)

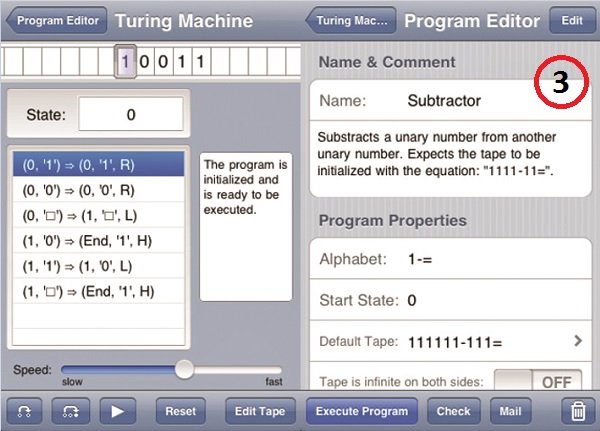
یک نمونه جالب دیگر از شبیه‌سازی‌های نرم‌افزاری از ماشین‌های تورینگ، شبیه‌سازی مخصوص iOS آن است که از طریق فروشگاه App Store قابل دانلود است. این برنامه، علاوه بر اجرای عملیات ماشین تورینگ به‌صورت بصری، برنامه‌های پیش‌فرض و همچنین قابل ویرایشی را نیز به همراه توضیحات کاملی از عملکرد هر‌کدام در اختیارکاربر می‌گذارد. (شکل3)

مطلب پیشنهادی

رایگان دانلود کنید: کتاب الکترونیکی «یادگیری ماشینی؛ سفری به اعماق هوشمندی»

جدول ‌گذار حالت‌های این ماشین که برای 2 علامت و 3 حالت طراحی شده، در جدول 1 آورده شده است. در این جدول علامت P به معنای چاپ یک روی نوار بوده و L و R به ترتیب به معنای انتقال نوار به چپ و راست است. این جدول را می‌توان به‌صورت دیاگرام انتقال حالت نیز نشان داد. اگرچه جدول‌های بزرگ انتقال حالت بهتر است به‌صورت جدولی باقی بمانند و این گونه قابلیت فهم بالاتری دارند، با این حال نمایش وضعیت ماشین‌های ساده به‌صورت دیاگرامی می‌تواند درک بهتر و ساده‌تری از آن‌ها را ارائه کند. توجه داشته باشید که دیاگرام‌های انتقال حالت، یک تصویر فریز‌‌شده از جدول عملکرد ماشین در زمان است و نباید آن را منحنی عملکرد محاسبات ماشین در طول زمان و مکان دانست. شکل 1 نمایی از دیاگرام انتقال حالت ماشین سه حالته Busy Beaver را نشان می‌دهد. با این حال، هر بار که ماشین Busy Beaver شروع به کار می‌کند، یک منحنی عملکردی را از آغاز تا پایان می‌پیماید اما یک ماشین کپی‌کننده که می‌تواند پارامترهای ورودی متغیر داشته باشد، ممکن است منحنی متفاوتی را طی کند. برای تعیین نحوه عملکرد صحیح یک ماشین در طول زمان به سادگی می‌توان از دیاگرام پیشرفت محاسبات استفاده کرد که نمونه‌ای از آن برای ماشین 3 حالته Busy Beaver در شکل 2 آورده شده است. 

ماشین تورینگ کوانتومی

ماشین تورینگ کوانتومی (QTM) و همچنین ماشین جامع تورینگ کوانتومی، ماشیني انتزاعی است که با بهره‌گیری از قدرت رایانش کوانتومی برای مدل‌سازی ساده کامپیوترهای کوانتومی مورد استفاده قرار می‌گیرد. 
در اصل، می‌توان هر الگوریتم کوانتومی را با یک ماشین تورینگ کوانتومی تفسیر و تشریح کرد. چنین ماشین‌هایی برای نخستین‌بار در سال 1985 و در یک مقاله از طرف دیوید دویچ (David Deutsch) فیزیکدان در دانشگاه آکسفورد مطرح شد. وی در این مقاله تلاش داشت تا نشان دهد گیت‌های کوانتومی می‌توانند همانند نمونه‌های سنتی دیجیتال با منطق دودویی نیز کار کنند. می‌توان ماشین‌های تورینگ کوانتومی را با استفاده از ماتریس‌های انتقالی خاص که توسط لنس فورت‌نو (Lanc Fortnow) تهیه و تدوین شده‌اند، به انواع کلاسیک و احتمالاتی ماشین‌های تورینگ مرتبط کرد. 
همچنین، نمونه‌هایی از چنین ماشین‌هایی تحت عنوان Linear Quantum Turing Machine توسعه داده شده است که کلیت یافته ماشین‌های معمولی کوانتومی تورینگ بوده و علاوه بر مدل‌سازی مفهوم حالات ترکیبی، امکان استفاده از توابع غیر قابل بازگشت را نیز فراهم می‌سازند. نتیجه استفاده از چنین ماشین‌هایی، ارزیابی کوانتومی بدون وجود عواقب کلاسیک آن است که در نوع خود بسیار ارزشمند است. لازم به ذکر است با این‌که ماشین‌های تورینگ کوانتومی مدلی ساده و جالب برای تحلیل الگوریتم‌های کوانتومی هستند اما مدارهای کوانتومی که از لحاظ محاسباتی با آن‌ها معادل هستند، بیشتر مورد استفاده قرار می‌گیرند.
 با مراجعه به آدرس www.mathematica-journal.com/issue/v8i3/features/hertel/index.html می‌توانید یک شبیه‌ساز ماشین کوانتومی تورینگ را که با استفاده از Mathematica توسعه داده شده است، دانلود کرده و برای آشنایی بیشتر با QTM از آن استفاده کنید.

نکته قابل توجه در تئوری مطرح شده از طرف تورینگ این است که وی‌ در مقاله اولیه خود میان «ماشین اتوماتیک» یا a-Machine و «ماشین انتخاب کننده» یا c-Machine تفاوت قائل بوده است چراکه در بخشی از نوشتار خود ذکر کرده است «حرکات ماشین خودکار، به‌طور کامل در پیکربندی تعیین شده است اما حرکات ماشین انتخاب کننده، به‌طور نسبی در پیکربندی آن تعیین شده است. زمانی که چنین ماشینی به یکی از این حالت‌های مبهم می‌رسد، باید تا زمان تعیین یک انتخاب از طرف عامل بیرونی منتظر باقی بماند. این می‌تواند در زمینه استفاده از ماشین‌ها در سیستم‌های axiomatic کاربرد داشته باشد.» 

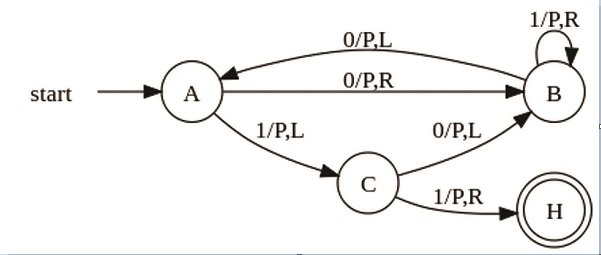
شكل1: نمای شماتیک جدول‌گذار Busy Beaver

مطلب پیشنهادی

رایانش کوانتومی در خدمت هوش مصنوعی

در انتظار یادگیری ماشینی کوانتومی خواهیم بود

در کنار این دو ماشین، وی صحبت از وجود نوع دیگری از ماشین را به میان می‌آورد که از آن‌ها به Oracle Machine (ماشین پیشگو) یا o-Machine تعبیر می‌شود. ماشین پیشگو، ماشین تورینگی است که محاسبات خود را برای تکمیل کردن، در حالت o متوقف می‌کند. در این حالت، این ماشین تا زمان تصمیم‌گیری توسط پیشگو(که مفهومی نامشخص بوده و شاید نتوان آن را ماشین به شمار آورد)منتظر می‌ماند. این ایده هم‌اکنون به شدت مورد توجه و استفاده ریاضیدانان است. 
یکی از کاربردهای چنین مفاهیمی، امور مرتبط با رمزنگاری است که در آن، پیشگوها برای استدلال در زمینه امنیت پروتکل‌های رمزنگاری در هنگام استفاده از توابع Hash به‌کار می‌روند. در این حالت، یک پیشگوی تصادفی به‌جای یک تابع Hash به طور متناوب به پرس‌و‌جوها پاسخ داده و از این طریق، میزان‌کاهش امنیت پروتکل مربوطه محاسبه می‌شود. 
دسترسی به پیشگوی تصادفی مذکور همانند تابع Hash برای تمام استفاده‌کنندگان، حتی حمله‌کنندگان فراهم خواهد بود. چنین کاری باعث می‌شود که حمله کنندگان با حل مسئله بسیار مشکلی در قلب مسئله کاهش امنیت مواجه بوده و نتوانند به راحتی از تابع Hash برای رسیدن به اهداف خود بهره ببرند. 
بیشتر گفته می‌شود که ماشین‌های تورینگ قدرتی مشابه با ماشین‌های واقعی دارند و می‌توانند هر عملیاتی را که یک برنامه واقعی می‌تواند انجام دهد، به انجام برسانند. چیزی که در این ادعا در نظر گرفته نشده آن است که ماشین‌های واقعی می‌توانند در هر لحظه در یکی از پیکربندی‌های متناهی خود قرار گیرند و در اصل، یک ابزار اتوماتیک شده خطی محدود هستند در حالی که ماشین‌های تورینگ فضای ذخیره‌سازی نامحدودی برای محاسبات خود در اختیار دارند. در اصل، ماشین تورینگ برای مدل‌سازی کامپیوتر کاربرد ندارد بلکه هدف اصلی آن‌ مدل‌سازی خود مفهوم محاسبات است. از لحاظ تاریخی نیز کامپیوترهایی که به محاسبات روی حافظه درونی خود می‌پرداختند، خیلی بعدتر از مطرح شدن ایده ماشین تورینگ ساخته شدند. در نقطه مقابل، دلایل بسیاری وجود دارد که بتوان از ماشین تورینگ برای مدل‌سازی کامپیوترهای واقعی استفاده کرد. شماری از این دلایل عبارتند از:
- هر کاری که یک کامپیوتر واقعی می‌تواند انجام دهد، یک ماشین تورینگ نیز می‌تواند. ماشین تورینگ می‌تواند هر نوع روالی که در زبان‌های برنامه‌نویسی پیدا می‌شود از جمله روال‌های بازگشتی و متدهای پردازش پارامترها را شبیه‌سازی کند. 
- ماشین تورینگ برخلاف کامپیوتر می‌تواند حجم نامتناهی از داده‌ها را پردازش کند که در صورت در نظر گرفتن زمانی محدود برای کارکرد آن، حجم داده‌های آن نیز همانند کامپیوتر محدود می‌شود. 
- همانند ماشین تورینگ، کامپیوترها می‌توانند فضای ذخیره‌سازی خود را با استفاده از انواع ابزارها و فناوری‌ها افزایش داده و به طور مناسب به انجام محاسبات بپردازند. 
- توصیف یک ماشین واقعی با استفاده از مفاهیم مجرد ساده‌تر، بسیار مشکل‌تر از توصیف آن‌ها با ماشین‌های تورینگ است. به عنوان مثال، شاید توصیف یک الگوریتم با مدل ماشین تورینگ با صدها حالت قابل انجام باشد در حالی که انجام چنین کاری با یک ماشین واقعی، صدها میلیون حالت مختلف را در بر داشته باشد. 
- ماشین‌های تورینگ الگوریتم‌ها را بدون توجه به میزان حافظه‌ای که مصرف می‌کنند، توصیف می‌کنند در حالی که همواره در زمینه میزان حافظه در دسترس ماشین‌های واقعی محدودیت‌های بسیاری وجود دارد. ماشین تورینگ این امکان را فراهم می‌کند که بی‌محدودیت، الگوریتم‌ها را بررسی کرده و به مشاهده نتایج عملکرد آن‌ها بپردازیم بدون این‌که در زمینه محدودیت‌های سیستم‌های واقعی نگرانی داشته باشیم.
- ماشین تورینگ فهم و تحلیل الگوریتم‌ها را ساده می‌کند. الگوریتم‌های معادلی که روی ماشین‌های مجرد معادل با ماشین تورینگ اجرا می‌شوند، عموماً در مقابل نمونه‌های مشابه خود در سیستم‌های واقعی کلیت بیشتری داشته و به‌عنوان مثال، معضلات مرتبط با انواع دقیق داده‌ای در آن‌ها مطرح نیست. 

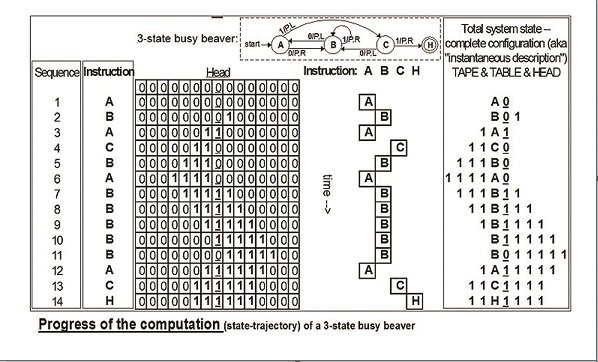
شكل2 : نمونه دیاگرام پیشرفت محاسبات یک ماشین Busy Beaver  سه حالته 

برای مطالعه قسمت‌ بعد روايت شكسته‌شدن كدهای انيگما در جنگ جهانی دوم روی لینک‌های زیر کلیک کنید:

مطلب پیشنهادی

ایده ماشین تورینگ چگونه مطرح شد و چه چیزی را دنبال می‌کرد؟ (بخش پایانی)