Bootstrap چه نقشی در دنیای علم داده‌ها دارد؟

با توجه به این‌که بوت استرپ در علم داده‌ها یک تکنیک پایه و کاربردی است، در این مطلب قصد داریم نحوه پیاده‌سازی آن با زبان برنامه‌نویسی پایتون را بررسی کنیم. این اصطلاح توسط آمارشناس فقید بردلی افرون ابداع شد. او قصد داشت نشان دهد که عمل محاسبه خطای برآوردکننده بدون دانستن توزیع آن به سختی صورت می‌گیرد، اما روش او به سادگی و به صورت یک رویکرد تکرارشونده ثابت قابل اجرا است. راهکاری که تا به امروز  نشان داده قادر است تقریب خوبی را ارائه کند.  

Bootstrap در دنیای علم داده‌ها و پیاده‌سازی آن با پایتون

‌بوت استرپ در علم داده‌ها راهکاری قدرتمند و مبتنی بر کامپیوترها است که برای استنباط آماری بدون تاکید بر فرضیه‌های زیاد استفاده می‌شود. راهکار فوق اجازه می‌دهد از یک نمونه داد یک توزیع نمونه‌برداری را ایجاد کرد. برای استنباط آماری در بوت استرپ ضرورتی ندارد تا اطلاعاتی از توزیع آماری برآوردگر در اختیار داشته باشید. در نتیجه بوت استرپ برای ایجاد فاصله اطمینان (Confidence Interval)، مدل رگرسیون (Regression Model) و یادگیری ماشین به شکل گسترده‌ای استفاده می‌شود. در این مقاله ما در ارتباط با دو موضوع مرتبط با بوت‌استرپ در علم داده‌ها یعنی ساخت فاصله اطمینان و انجام آزمون فرض آماری مطالبی در اختیارتان قرار می‌دهیم. با این‌حال هر یک از این موارد یاد شده را می‌توان به کمک روش‌های صریح آماری و به کمک بوت‌استرپ پیاده‌سازی کرد و نتایج به‌دست آمده را با یکدیگر مقایسه کرد. با توجه به گستردگی زبان پایتون در پیاده‌سازی روش‌های مطرح شده در علم داده، کدهایی نیز با استفاده از این زبان نوشته‌ شدهراند تا اجرای محاسبات و عملیات مرتبط با آن‌ها نیز معرفی شوند.

ایجاد فاصله اطمینان با بوت‌استرپ در علم داده‌ها

‌در دنیای واقعی، به شکل دقیق و روشن اطلاعات چندانی در ارتباط با جامعه آماری و ویژگیرهای متغیرهای آن‌ها در اختیار نداریم. به‌طور مثال، جامعه آماری ممکن است کل جمعیت کره زمین یا معاملات انجام گرفته روز گذشته بازار سهام یا گردش مالی حال و آینده یک شرکت باشد. مشکل اصلی این است که به دلیل بزرگ بودن اندازه جامعه آماری، در بیشتر موارد مجبور به نمونه‌گیری هستیم تا تخمین دقیقی برای ویژگی‌های آماری جامعه به دست آوریم. به بیان ساده‌تر، برای استنباط و به‌دست آوردن اطلاعاتی در مورد پارامترهای مربوط به جمعیت هدف مجبور هستیم به توزیع نمونه اعتماد کنیم. برای پیاده‌سازی آزمون فرضیه و نحوه ساخت فواصل اطمینان روش‌های مختلفی در دسترس قرتر دارند که از آن جمله می‌توان به آزمون تی‌تک نمونه‌ای (T-Test)، آزمون t دو نمونه (Two sample t-test)، آزمون Z (Z-test) و آزمون مجذور کای (Chi-squared Test) اشاره کرد. یک جایگزین ناپارامتری برای هر یک از موارد یاد شده به‌کارگیری تکنیک Bootstrapping است. در این مطلب برای روشن‌ شدن بحث مثالی را بررسی می‌کنیم تا ببینیم چگونه از توزیع نمونه برای ساخت فاصله اطمینان برای پارامتر موردنظر خود باید استفاده کنیم. به بیان ساده‌تر، هدف این است که ایده‌ای در ارتباط با متوسط قد افرادی که قهوه می‌نوشند به‌وسیله نمونه‌های گرفته شده به‌دست آوریم.

راهکار اول: با استفاده از تکنیک Bootstrapping

در این‌جا فرض می‌کنیم که یک مجموعه داده از تمامی افرادی که قهوه می‌نوشند در اختیار داریم و در فایلی به‌نام coffee_full.csv ذخیره کرده‌ایم. این فایل فشرده از این آدرس قابل دریافت است. پس از آن‌که فایل فوق را از حالت فرشده خارجی کردید با استفاده از کد زیر آن‌را فراخوانی کنید

coffee_full = pd.read_csv(‘coffee_full.csv’)

قابل فایل‌های .csv سرنام Comma Separated Values مرتبط با فایل‌های اطلاعاتی است که ستون‌های متغیرها در آن‌ها با استفاده از علامت سجاوندی کاما از یکدیگر جدا شده‌اند. با استفاده از دستور زیر یک مجموعه داده به شکل نمونه‌ای 200‌ تایی از پایگاه داده coffee full ایجاد می‌کنیم. این مجموعه داده‌ را coffee_red نام‌گذاری می‌کنیم. از این پس از نمونه یاد شده برای انجام محاسبات استفاده می‌کنیم. در این‌جا ما یک نمونه از جامعه واقعی ایجاد کرده‌ایم.

coffee_red = coffee_full.sample(n=200)

اکنون دستورات زیر را در نظر بگیرید. با استفاده از قطعه کد زیر نسبت افرادی که قهوه می‌نوشند در پایگاه داده ما محاسبه و در خروجی ظاهر می‌شود.

[coffee_red[‘drinks_coffee’]==True].mean()

---Output---

0.595

در کد پایین نیز میانگین ارتفاع یا قد افراد بر حسب اینچ محاسبه شده است.

coffee_red[coffee_red[‘drinks_coffee’]==True]['height'].mean()

---Output---

68.119 inches

اکنون بر مبنای کد زیر از تکنیک بوت استرپ در علم داده‌ها استفاده می‌کنیم و یک فاصله اطمینان برای میانگین ایجاد می‌کنیم.

# Let's first create an empty list for storing means of bootstrapped samples

boot_means = []

# Let's write a loop for creating 1000 bootstrapped samples

for i in range(1000):

    bootsample = coffee_red.sample(200, replace=True)

    bootsample_mean = bootsample.[bootsample[‘drinks_coffee’]==True]['height'].mean()

    boot_means.append(bootsample_mean)

boot_means = np.array(boot_means)

برای حصول اطمینان 95 درصد یا در حقیقت 5 درصد خطا بر اساس 100 بار نمونه‌گیری، میانگین را تخمین‌ می‌زنیم. از بیان آن‌ها 2.5 درصد از آن‌هایی که کمترین مقدار را دارند حذف می‌کنیم. همچنین در میان آن‌هایی که بزرگرترین مقادیر را دارند نیز 2.5 درصد را حذف می‌کنیم. میانگین‌های باقی‌مانده یک فاصله اطمینانی با ضریب 95 درصد را ایجاد می‌کنند. به بیان ساده‌تر کران پایین و بالای این میانگین‌ها همان فاصله اطمینان 95 درصدی برای میانگین جامعه آماری است.

# we build 95% in the middle portion

np.percentile(boot_means, 2.5), np.percentile(boot_means, 97.5)

---Output---

(66.00, 67.59)

فاصله اطمینانی که در کد بالا ایجاد شده را می‌توان کران‌های میانگین برای قد افراد جامعه با اطمینان 95 درصد توصیف کرد. دستور percentile صدک‌ها را مشخص می‌کند. به همین علت صدک 2.5 و 97.5 را مشخص کرده‌ایم. (در آمار صدک (Percentile) به مقداری گفته می‌شود که درصد خاصی از نمونه‌های یک متغیر تصادفی کم‌تر از آن هستند. به‌طور مثال ۲۰امین صدک یک متغیر تصادفی مقداری است که ۲۰ درصد از مشاهدات این متغیر کم‌تر از آن هستند. ۲۵امین، ۷۵امین صدک یک متغیر نام‌های خاص چارک اول و چارک سوم را دارند. صدک دهم را دهک اول هم می‌نامند.)

برای نمایش این فاصله اطمینان از یک نمودار فراوانی استفاده می‌کنیم. کدی که در ادامه مشاهده می‌کنید برای نمایش فراوانی میانگین‌های تولید شده توسط بوت استرپ است. ناحیه‌ای که مسافتی برابر با 95 درصد کل نمودار را به صورت متقارن از مرکز داده دارد همان فاصله اطمینان است.

plt.hist(boot_means, alpha=0.7);

plt.axvline(np.percentile(boot_means, 2.5), color='red', linewidth=2) ;

plt.axvline(np.percentile(boot_means, 97.5), color='red', linewidth=2) ;

شکل زیر نمودار فراوانی حاصل را نشان می دهد.

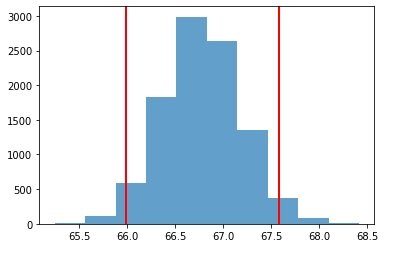
تفسیر فاصله اطمینان

فاصله اطمینان، تعیین کران‌های تصادفی است که با استفاده از آن‌ها سطح اطمینان مشخصی، می‌توانیم پوششی برای میانگین جامعه ایجاد کنیم. به بیان ساده‌تر، می‌گوییم با اطمینان 95 درصد مطمئن هستیم که بازه (66.0,67.59) شامل میانگین جامعه یعنی میانگین قد افرادی است که قهوه می‌نوشند. در قطعه کد زیر نحوه محاسبه میانگین جامعه آماری مشخص شده است.

coffee_full[coffee_full[‘drinks_coffee’]==True][‘height’].mean()

---Output---

66.44 inch

کاملا بدیهی است که بازه ارائه شده یعنی 66.0,67.59 شامل مقدار 66.44 است.

راهکار دوم، ساخت فاصله اطمینان با استفاده از آزمون فرض آماری (t-Test)

راهکارهای دیگری نیز برای محاسبه فاصله اطمینان آماری برای پارامتر جامعه وجود دارد. این‌کار به ویژه هنگام به‌کارگیری استفاده از توابعی که آزمون مربوط به میانگین را انجام می‌دهند قابل اجرا است. کدی که با استفاده از پایتون برای انجام آزمون مقایسه میانگین نوشته‌ایم را در ادامه مشاهده می‌کنید. در بخش cm.tconfint_diff برای اختلاف میانگین قد دو گروهی که در نمونه coffee_red و غیر از آن هستند یک فاصله اطمینان ساخته شده است.

import statsmodels.stats.api as sm

X1 = coffee_red[coffee_red['drinks_coffee']==True]['height']

X2 = coffee_red[coffee_red['drinks_coffee']==False]['height']

cm = sm.CompareMeans(sm.DescrStatsW(X1), sm.DescrStatsW(X2))

print (cm.tconfint_diff(usevar='unequal'))

با اجرای قطعه کد فوق مشاهده می‌کنیم که اختلاف ناچیزی میان نتیجه فاصله اطمینان با استفاده از تکنیک بوت استرپ و روش مستقیم آماری وجود دارد که ناشی از ناپارامتری بودن روش بوت استرپ است. روشن است که روش مستقیم به شرطی که توزیع داده‌ها واضح باشد دقیق‌تر و قابل استنادتر است. اکنون به نظر می‌رسد اندازه فاصله اطمینان که شامل تفاضل کران بالا و پایین است در روش مستقیم کوچک‌تر از روش بوت استرپ باشد.

آزمون فرض آماری و Bootstrap در علم داده‌ها

به عنوان یک تحلیل‌گر داده‌ها باید در ارتباط با مفهوم آزمون فرض و فرضیه آماری دانش کافی داشته باشید. آزمون فرض آماری، تکنیکی است که با استفاده از آن‌ نسبت به پارامتر جامعه هدف، دو فرضیه استفاده می‌شود و طبق نتایج به‌دست آمده از نمونه‌گیری نسبت به رد یا تایید یکی از آن‌ها اقدام می‌کنیم.

با توجه به آزمون فرض آماری، در مورد میانگین قد افراد در نظر داریم فرضیه‌‌ای ارائه کرده و طبق نمونه‌ای که گرفته‌ایم، فرضیه‌ها را تایید یا رد کنیم. دقت کنید که در نظر داریم بدانیم آیا متوسط قد افرادی که قهوه می‌نوشند از 70 اینچ بلندتر است یا خیر. همان‌گونه که می‌دانید آزمون فرضد آماری از دو فرضیه به‌نام‌های فرض صفر و فرض مقابل ساخته شده است. برای مسئله ما، این فرضیه‌ها را به صورت زیر در نظر می‌گیریم:

دقت کنید که به‌طور معمول نظری که از قبل موجود باشد در فرض صفر یا فرض تهی (Null Hypothesis) نوشته می‌شود و فرضیه موردنظر برای تحقیق که برعکس نظریه قبلی است به عنوان فرض جایگزین (Alternative Hypothesis) نوشته می‌شود.

اکنون برای تصمیم‌گیری نسبت به درست بودن هر یک از فرضیه‌ها از دو روش استفاده می‌کنیم. در ابتدا با تکیه بر تکنیک بوت‌استرپ در علم داده‌ها فرضیه‌ها را آزمایش می‌کنیم و در ادامه با تکنیک‌های شبیه‌سازی صحت فرض صفر را ارزیابی می‌کنیم.

راهکار اول: بررسی امکان‌پذیر بودن فرض صفر با استفاده از Bootstrap

در این بخش با 1000 مرتبه شبیه‌سازی داده‌ها و محاسبه میانگین نمونه‌ای، یک توزیع نمونه‌ای و فاصله اطمینان برای میانگین جامعه ایجاد می‌کنیم. ما از این موضوع مطلع هستیم که اگر فاصله اطمینان تولید شده مطابق با فرض صفر باشد آن فرض تایید شده است. همچنین اگر فاصله اطمینان با فرض مقابل هماههنگ باشد فرض صفر را رد و فرض مقابل یا همان جایگزین را تایید می‌کنیم.

means = []

for i in range(10000):

   bootsample = sample_df.sample(n=150, replace = True)

   bootsample_mean = bootsample[bootsample['drinks_coffee']==True]

   means.append(bootsample_mean['height'].mean())

means = np.array(means)

np.percentile(means, 2.5), np.percentile(means, 97.5)

---Output---

(66.00, 67.59

همان‌گونه که مشخص است فاصله اطمینان 95 درصد تولید شده با کران‌های 66.0 و 67.59 به‌دست آمده است. مقدار 70 که در فرض مقابل به آن اشاره شد، در این محدوده قرار نمی‌گیرد و بازه کوچک‌تر از 70 است. در نتیجه دلیلی مبنی بر رد فرض صفر وجود ندارد و فرض جایگزین رد می‌شود.

راهکار دوم شبیه‌سازی فرضیه صفر

فرض کنید که فرضیه صفر در آزمون فرض آماری درست باشد. به این ترتیب اگر از توزیع عادی با توجه به این فرض شبیه‌سازی و مقادیر زیادی تولید کنیم، انتظار داریم که میانگین نمونه‌های آن‌ها نزدیک باشد و فرض صفر تایید شود. در دستور زیر به شبیه‌سازی از توزیع عادی با میانگین 70 و انحراف معیار میانگین‌ها پرداخته‌ایم.

null_vals = np.random.normal(loc = 70, scale = np.std(means), size =10000)

در هر مرتبه نمونه‌‌گیری یک میانگین تولید می‌شود که بر مبنای فرض صفر ساخته شده‌اند. با استفاده از تکنیک شبیه‌سازی می‌توان به این پرسش پاسخ داد که میانگین نمونه‌ای در توزیع عادی مربوطه در کجا قرار می‌گیرد.

plt.hist(null_vals, alpha=0.7);

plt.axvline(sample_mean, color = 'red', linewidth=2);

خروجی قطعه کد فوق در تصویر زیر نشان داده شده است:

با توجه به فرضیه‌های آماری بیان شده، مشخص است که باید فرض صفر را تایید و فرض جایگزین را رد کرد.

p_value = (null_vals > sample_mean).mean()

p_value

--Output--

1.0

مقادیر بزرگ برای p-value بیان‌گیر تایید فرض صفر هستند و دلیلی برای رد فرض صفر نیستند. به این شکل به نظر میررسد که میانگین جامعه در ارتباط با افرادی که قهوه می‌نوشند کمتر یا برابر با 70 اینچ است. در ارتباط با p-value لازم است به چند نکته مهم زیر دقت کنید:

یکی از مهم‌ترین مسائل موجود در آمار استنباطی، آزمون فرض‌های آماری است که در تصمیم‌گیری بسیار حائز اهمیت است. یکی از مسائل موجود در آزمون فرض ارائه یک معیار برای پذیرفتن یا رد فرض است. یکی از معیارهایی که جهت انجام آزمون فرض معرفی شده‌، مقدار-P است.

فرض آماری

یک فرض آماری ادعایی در مورد یک یا چند جمعیت مورد بررسی است که ممکن است درست یا نادرست باشد. به عبارت دیگر فرض آماری ادعا یا گزاره‌ای در مورد توزیع یک جمعیت یا پارامتر توزیع یک متغیر تصادفی است.

آزمون آماری

برای بررسی یک فرض آماری یک آزمایش تصادفی انجام می‌دهیم (جمع آوری داده‌ها). اگر نتیجه آزمایش تفاوت «معنی داری» با آنچه که انتظار داریم، داشته باشد وقتی که فرض مورد نظر را صحیح فرض کرده‌ایم، فرض را رد می‌کنیم و در غیر این صورت نمی‌توانیم آن را رد کنیم.

آماره آزمون

هر آزمون آماری معمولاً بر حسب یک آماره بیان می‌شود که این آماره، آماره آزمون نامیده می‌شود.

ناحیه رد و پذیرش

فرض کنید آماره آزمون دارای فضای برد R باشد. اگر C یک زیرمجموعه از R برای رد فرض آزمون باشد، آنگاه C ناحیه رد یا بحرانی نامیده می‌شود. مکمل مجموعه C را ناحیه پذیرش می‌نامیم.

فرض صفر و فرض مقابل

هر آزمون آماری باید شامل دو فرض مکمل هم باشد. به طور متعارف فرض مورد آزمون، فرض صفر نامیده و با H0 نمایش داده می‌شود، فرضی که مکمل فرض صفر است، فرض مقابل نامیده می‌شود و با H1 نشان می‌دهیم.

خطاهای آزمون فرض و احتمال آنها

نتیجه یک آزمون فرض ممکن است ما را در تصمیم گیری دچار اشتباه نماید. اگر وقتی فرض صفر صحیح است، با استناد به نتیجه آزمایش آن را رد کنیم، مرتکب خطای نوع اول شده‌ایم. همچنین در صورتی که فرض صفر را وقتی که اشتباه است، بپذیریم، خطای نوع دوم رخ داده‌است.

به لحاظ تصویری: p-value سطح زیر منحی مربوط به تصویر بالا است که در سمت راست خط قرمز رنگ قرار دارد. با توجه به این‌که تمامی مقادیر در سمت راست خط قرمز هستند، تمامی مقادر در تایید فرض صفر سهم دارند و دلیلی برای رد فرض صفر وجود ندارد.

در این‌‌جا p-value  را به عنوان میانگین تعداد حالت‌هایی تصور می‌کنیم که نمونه‌های استخراج یا شبیه‌سازی شده از توزیع عادی با میانگین 70 و انحراف معیار برابر با انحراف معیار نمونه از مقدار میانگین نمونه‌ای که برابر با 67.5 است بیشتر است.