تکنیک عقبگرد
تکنیک عقب گرد (Backtracking) شیوهای در حل مسائل است که از علامتهای خاصی برای بیان اینکه راه حل کاندیدی به حل مسئله می انجامد یا خیراستفاده میکند.این رویکردبرای حل مسائل درخت فضای آن مسئله راایجاد کرده و تعیین میکند کدام گره امید بخش است. الگوریتمهای عقب گردی از تابلوها یا علامتهایی برای بیان اینکه یک راه حل کاندید به حل مسئله نمیانجامد استفاده میکند. عقبگرد، حالت اصلاح شده جستجوی عمقی یک درخت میباشد. مثال اول در روش عقب گرد مسئله قفل رمزی میباشد.یک قفل رمزی شامل n کلید دیجیتالی است که هر کلید فقط دو حالت بسته (1) یا حالت باز (0) دارد. می دانیم که n کلید دیجیتالی تعداد 2nحالت مختلف را پدید میآورند و این قفل تنها با یک حالت که همان رمز است باز میشود.
مثال دوم در روش عقب گرد مسئله چند وزیر میباشد.هدف این مسئله چیدن n وزیر در یک صفحه شطرنج n*n است به گونهای که هیچ دو وزیری یکدیگر را تهدید نکنند.
مثال سوم در حل مسئله رنگ آمیزی گراف میباشد.در این مسئله می خواهیم تمام راههای ممکن جهت رنگ آمیزی گرههای یک گراف بدون جهت را با استفاده از حداکثر m رنگ متفاوت پیدا کنیم، به گونهای که هیچ دو رأس مجاوری هم رنگ نباشند.
مثال چهارم مسئله حاصل جمع زیر مجموعه ها میباشد .در این مسئله، n عدد صحیح مثبت wi و یک عدد صحیح مثبت w داریم . هدف پیدا کردن تمامی زیر مجموعههایی از این اعداد صحیح میباشد که حاصل جمع آنها بربر w است.
پیمایش درخت
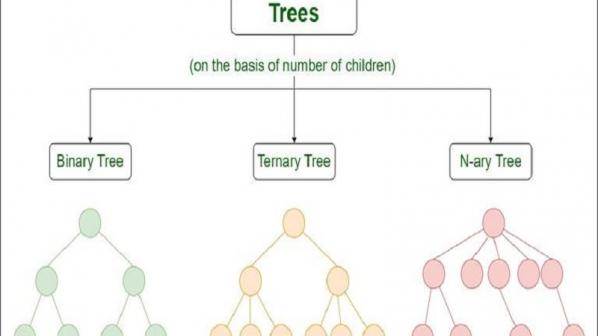
در علم کامپیوتر پیمایش درخت شکلی از پیمایش گراف است و به پروسه ملاقات گرهها در ساختمان داده درخت اشاره دارد، به نحوی که ر گره دقیقاً یکبار ملاقات شود. اینگونه پیمایشها به ترتیب گرهای که ملاقات میکنند دستهبندی شدهاند. الگوریتمهای زیر برای یک درخت دودویی شرح داده شدهاند اما ممکن است قابل تعمیم به سایر درختها نیز باشند.
انواع
در مقایسه با ساختمان دادههای خطی مانند لیستهای پیوندی و آرایه یک بعدی که یک روش پیمایش استاندارد دارند؛ ساختارهای درختی میتوانند در مسیرهای مختلفی پیمایش شوند. برای شروع از ریشه یک درخت دودویی سه گام اصلی وجود دارد که ترتیب انجام آنها نوع پیمایش درختی را مشخص میکند. این مراحل عبارتند از: انجام یک عمل در گره فعلی که اشاره به دیدن گره دارد، پیمایش به سمت گره فرزند چپ و پیمایش به سمت گره فرزند راست در برخی از روشها پیمایش شامل تکرار همه گرهها میشود. چراکه از گره داده شده ممکن است بیش از یک گره بعدی وجود داشته باشد( در این حالت آن ساختمان داده خطی نیست) پس با فرض محاسبه متوالی (نه موازی) بعضی از گرهها باید در برخی مسیرها به تعویق بیفتند و برای ملاقاتهای بعدی ذخیره شوند. این کار اغلب بواسطه پشته و از طریق الگوریتم LIFO یا از طریق صف و از طریق الگوریتم FIFO انجام میشود. ساختمان داده همانند یک درخت بازگشتی است، پیمایش میتواند به عنوان یک بازگشت تعریف شود، در یک مد طبیعی و روشن گرههای معوق به صورت ضمنی در پشته تماس ذخیره میشوند. نامی که به پیمایشها داده میشود از ترتیبی که آنها گرهها را ملاقات میکنند گرفته شدهاست. به بیان سادهتر پیشروی به سمت پایین (اول-عمق، فرزند اول سپس نوه، قبل از فرزند دوم ) یا اول-سطح (اول سطح یا عرض، فرزند اول سپس فرزند دوم قبل از نوه) پیمایشهای اول –عمق بیشتر بر اساس وضعیت عناصر ریشه با توجه به گرههای موجود در سمت چپ و راست دستهبندی شدهاند. تصور کنید که گره چپ و راست در مکان خود ثابت هستند، پس گره ریشه میتواند در طرف چپ گره سمت چپ قرار داده شود (پیمایش پیشوندی) یا اینکه بین گره راست و چپ قرار گیرد (پیمایش میانوندی) یا طرف راست گره سمت راست باشد (پیمایش پسوندی). هیچگونه اختلاف مشابهی در پیمایش اول-سطح که به گره فرزند نسبت داده شده وجود ندارد؛ در نتیجه پیمایش اول-سطح بی ابهام و واضح است. برای طراحی همیشه فرض بر این است که گرههای سمت چپ بر گرههای سمت راست مقدم هستند. این مرتبسازی میتواند تا زمانی که همین ترتیب برای همه روشهای پیمایش، درنظرگرفته وارونه شود. پیمایش اولعمق از طریق پشته به آسانی قابل پیادهسازی است، در حالی که اولسطح به سادگی از طریق صف قابل پیادهسازی است. فراتر از این پیمایشها عمومی طرحهای پیچیدهتر و ترکیبی مختلفی نیز قابل پیادهسازی است، نظیر جستجوهای عمق محدود (depth- limited)، جستجوی تعمیق تکراری (iterative deepening depth-first). میخواهیم با حرکت روی یالهای یک درخت، همه گرههای آن را هر کدام یک بار ملاقات کنیم. به این کار پیمایش درخت میگویند. بسته به این که کدام عنصر، کی ملاقات شود، پیمایش درخت لیست یا یک ترتیب خطی از عناصر آن درخت به ما میدهد. طبیعتاً پیمایشهای متفاوت ترتیبهای متفاوتی خواهند داد. دو روش عمقل اول و سطح اول، دو روش معمول پیمایش درخت هستند که بیشتر برای پیمایش درخت دودویی به کار میروند.
عمق اول
اول-عمق Depth-first سه نوع پیمایش اول- عمق وجود دارد: پیمایش پیشوندی (Pre-Order)، پیمایش میانوندی (In-Order)، پیمایش پسوندی (Post- order) برای درخت دودویی، آنها در هر گره، با شروع از گره ریشه به عنوان عملیات بازگشتی تعریف شدهاند که الگوریتم آنها به شرح زیر است: پیمایش پیشترتیب:
ریشه را ملاقات کن.
زیر درخت چپ را پیمایش کن.
زیر درخت راست را پیمایش کن.
پیمایش میانترتیب:
زیردرخت چپ را پیمایش کن.
ریشه را ملاقات کن.
زیردرخت راست را پیمایش کن.
پیمایش پسترتیب:
زیر درخت چپ را پیمایش کن.
زیر درخت راست را پیمایش کن.
ریشه را ملاقات کن.
درخت عمومی
به منظور پیمایش هر درختی در پیمایش اول-عمق، عملیاتهای بازگشتی زیر در هر گره انجام میشود: ۱. انجام عمل پیمایش پیشوندی ۲. برای هر i (با i=1 to n) انجام میشود: ۱. ملاقات iام، اگر وجود داشته باشد. ۲. انجام عملیات پیمایش میانوندی ۳. انجام عملیات پیمایش پسوندی جایی که n تعداد گرههای فرزند است، وابسته به مشکلی که وجود دارد عملیات پیمایش پیشوندی، میانوندی و پسوندی ممکن است بیاعتبار شوند یا اینکه ممکن است شما بخواهید از یک گره فرزند خاصی بازدید کنید بنابراین این عملیاتها اختیاری هستند. همچنین در عمل ممکن است بیش از یک عملیات پیشوندی، میانوندی و پسوندی نیاز باشد. به عنوان مثال زمان وارد شدن به یک درخت سه تایی، یک عملیات پیشوندی بواسطه مقایسه، بخشها انجام شدهاست. ممکن است یک عملیات پسوندی پس از متوازن کردن مجدد درخت نیاز باشد.
اول سطح
درختها میتوانند به ترتیب هر سطح پیمایش شوند، به گونهای که همه گرهها در یک سطح را ملاقات میکنیم، سپس به ترتیب به سطوح پایینتر میرویم و تمام گرههای آنها را ملاقات میکنیم.
روشهای پیمایش دیگری هم وجود دارند که جزء هیچیک از دو روش بالا دستهبندی نمیشوند. جستجوی درختیِ مونته کاریو یکی از این روش هاست که روی محتملترین حرکات براساس توسعه درخت جستجو روی نمونهسازی تصادفی فضای محل جستجو بنا شدهاست.
درختهای بینهایت
با اینکه عموماً پیمایش روی درختهایی با تعداد گره محدود انجام میشود اما امکان پیادهسازی آن روی درختهای بینهایت و نامحدود نیز وجود دارد. حتی بعضی درختهای محدود نیز آنقدر بزرگند که میتوان به عنوان درختهای بینهایت آنها را مورد بررسی و آنالیز قرار داد مانند درخت بازی یا شطرنج. این یک علاقه خاص در برنامهنویسی تابعی است؛ بنابراین ساختمانهای داده بینهایت اگر (به شدت) مورد ارزیابی قرار نگرفتهاند اغلب میتواند تعریف شود و کار کند، در این صورت زمان بینهایتی خواهد برد. برخی ازدرختان محدود برای نمایش ساده بیش از حد بزرگ هستند نظیر درخت بازی، شطرنج، بازی گو و نظایرآن. این کاری سودمند و مفید است که آنها را به عنوان اینکه اگر آنها بینهایت بودند بررسی کنیم. یک نیاز اساسی برای پیمایش، ملاقات کردن هر گره است. برای درختان بینهایت الگوریتمهای ساده اغلب به شکست میانجامند. به عنوان مثال درخت دودویی داده شده با عمق بینهایت، پیمایش اول-عمق از یک سمت درخت پایین خواهد رفت (بنابر قانون سمت چپ). هیچگاه مابقی را ملاقات نخواهدکرد؛ و در واقع اگر پیمایش میانوندی و پسوندی هیچگاه گرهی را ملاقات نکنند پس باید به برگ رسیده باشند (ولی در واقعیت اینطور نیست). در مقابل، پیمایش اول-سطح (پیمایش سطحی) درخت دودویی با عمق بینهایت را بدون مشکل پیمایش میکند؛ و در واقع هر درخت را با فاکتور انشعاب محدود پیمایش میکند. به بیانی دیگر درختی با ۲ عمق داده شده که گره ریشه فرزندان بینهایت بسیاری دارد و هر یک از این فرزندان دو فرزند دارند، پیمایش اول-عمق تمامی گرهها را ملاقات میکند در مرتبه اول از گرههای نوه (فرزند فرزند هر گره) تهی میشود، سپس به سمت بعدی حرکت میکند (فرض میکنیم که آن پیمایش پسوندی نیست). در مقابل پیمایش اول- سطح هیچگاه به گره نوه نمیرسد، بنابراین آن به دنبال تهی کردن فرزند اول است. تجزیه و تحلیلهای پیچیده تری از زمان اجرا میتوانند از طریق اعداد ترتیبی نامحدود داده شوند؛ بنابراین جستجوهای اول-عمق یا اول-سطح پیمایشات درخت درخت بینهایت را انجام نمیدهند و برای درختان خیلی بزرگ کارآمد نیستند. به هر حال، پیمایشات ترکیبی میتواند درختان بینهایت (قابل شمارش) را پیمایش کنند مخصوصاً از طریق اثبات مورب («مورب» ترکیبی است از افقی و عمودی که سطح و عمق را مرتبط میکند). مشخصا، شاخههای درخت بینهایت داده شده با عمق نامحدود گره ریشه را با علامت ()، فرزندان گره ریشه را با علامت (۱)، (۲) و... نوهها را با علامت (۱٬۱)، (۱٬۲) و ... (۲٬۱)، (۲٬۲)، .... مشخص میکند. در نتیجه، گرهها در یک تناظر یک به یک با توالی محدودی از اعداد مثبتی هستند، که قابل شمارش اندو میتوانند برای مرتبه اول به وسیله مجموع ورودیها و سپس با رعایت ترتیب واژه نگاری بین جمع داده شده (تنها توالی محدود با مقادیر داده شده جمع میشوند بنابراین تمامی ورودیهایی که به صورت رسمی بدان دسترسی یافتهاست، یک تعداد متناهی از ترکیب یک عدد طبیعی داده شدهاست) که یک پیمایش را میدهد، جایگذاری شوند. این میتواند به عنوان نگاشت عمق بینهایت درخت باینری بر روی این درخت و سپس پیمایش اول-سطح تفسیر شود: جایگزینی ضلع پایینی متصل به گره والد به فرزندان دوم و بعدی خودش با ضلع سمت راست ازاولین فرزند به دومین فرزند و از دومین فرزند به سومین فرزند و ... . بنابراین در هر مرحله یک یا هر دو میتوانند به پایین (اضافه کردن یک (۱)) یا به راست (اضافه کردن یک (۱) به آخرین عدد) (بجز ریشه که اضافی است و میتواند به پایین برود) بروند، که ارتباط و مراسلات بین درخت دودویی بینهایت وشمارهگذاری بالا را نشان میدهد. مجموع ورودیها (منهای ۱) مربوط به فاصله از ریشه که برابر است با 2n-1 گره در عمق n-1 در درخت دودویی بینهایت.
تکنیک جستجوی فیبوناچی
در علوم رایانه، تکنیک جستجوی فیبوناچی یک راهی برای جستجو در آرایه مرتبشده با استفاده ار الگوریتم تقسیم و غلبه است که قسمتی که قرار است بررسی شود را با کمک اعداد فیبوناچی محدود میکند. در مقایسه با جستجوی دودویی، جستجوی فیبوناچی بخشهایی را مورد بررسی قرار میدهد که مقادیر انها به هم نزدیکتر است و پراکندگی کمتری دارند. وقتی یک عنصر جستجو میشود دسترسی غیر یکنواختی به حافظه دارد (یعنی زمان مورد نیاز برای دسترسی به فضای حافظه متغیر است و بستگی به مکانی دارد که مرحله قبل به آن دسترسی پیدا کرده). مزیت جستجو فیبوناچی نسبت به جستجوی دودویی در کاهش زمان متوسط مورد نیاز برای دسترسی به حافظه است. نوار مغناطیسی نمونهای از مثال دسترسی غیر یکنواخت به حافظهاست، زمان برای دسترسی به یک عنصر خاص بستگی به فاصله ان تا عنصری دارد که هماکنون زیر هد نوار است. توجه کنید که آرایههای بزرگ که درکش پردازنده یا حتی حافظه اصلی جا نمیشوند هم میتوانند به عنوان یک مثال از دسترسی غیر یکنواخت باشند. جستجوی فیبوناچی دارای پیچیدگی زمانی ((o(log(x است. جستجوی فیبوناچی در ابتدا توسط کیفر (kiefer) به عنوان روشی برای کم کردن خطاها (مینیماکس) در جستجو برای پیدا کردن بیشینه و کمینه در تابع با یک مد اختراع شد.
ماهنامه شبکه را از کجا تهیه کنیم؟
ماهنامه شبکه را میتوانید از کتابخانههای عمومی سراسر کشور و نیز از دکههای روزنامهفروشی تهیه نمائید.
ثبت اشتراک نسخه کاغذی ماهنامه شبکه
ثبت اشتراک نسخه آنلاین
کتاب الکترونیک +Network راهنمای شبکهها
- برای دانلود تنها کتاب کامل ترجمه فارسی +Network اینجا کلیک کنید.
کتاب الکترونیک دوره مقدماتی آموزش پایتون
- اگر قصد یادگیری برنامهنویسی را دارید ولی هیچ پیشزمینهای ندارید اینجا کلیک کنید.
























نظر شما چیست؟