تصور کنید، یک مسئله پیچیده در اختیار دارید که امکان حل آن با الگوریتمهای رایج فراهم نیست. در چنین شرایطی، چگونه باید یک الگوریتم کاربردی تعریف کرد تا در مرحله بعد به کدهای قابل استفاده تبدیل شود؟ هوش مصنوعی برای پاسخگویی به یک چنین مسائلی در دنیای واقعی به کار گرفته میشود. مسائلی که در اصطلاح تخصصی به آنها رامنشدنی میگوییم. به عبارت دقیقتر، زمانی از الگوریتمهای هوش مصنوعی استفاده میشود که الگوریتمهای عادی پاسخی برای یک مسئله نداشته باشند. یکی از موثرترین و سادهترین تکنیکهای حل مسائل در حوزه هوش مصنوعی، رویکرد محاسبات تکاملی است. یکی از مهمترین اهدافی که الگوریتمهای تکاملی به دنبال آن هستند، بهبود کیفیت راهحلهای ضعیف پیرامون یک مسئله هستند. برای بهبود کیفیت راهحلهای ضعیف، الگوریتمها و محاسبات تکاملی از فرآیندهای تکاملی همچون جهش (Mutation) و نمونههای مشابه استفاده میکنند. الگوریتمهای تکاملی در یک فرآیند تکرارشونده سعی میکنند از عملگرهایی همچون جهش برای دستکاری راهحلهای ضعیف استفاده کنند تا یک سامانه بتواند به مطلوبترین شکل ممکن یک مسئله را حل کند.
محاسبات تکاملی
محاسبات تکاملی تجسم یا به عبارت دقیقتر الهام گرفته شده از الگوریتمهای بهینهسازی سراسری (General Optimization) و فرآیندهای تکامل زیستی (Biological Evolution) هستند. متخصصان هوش مصنوعی الگوریتمهای محاسبات تکاملی را اینگونه توصیف کردهاند: «محاسبات تکاملی شاخهای از هوش مصنوعی و محاسبات نرم هستند که سعی میکنند از فرآیندهای تکامل زیستی برای پیدا کردن راهحلی برای مسائل استفاده کنند. محاسبات تکاملی مبتنی بر جمعیت (Population-based) و آزمون و خطا (Trial and Error) هستند و از بهینهسازی تصادفی (Stochastic Optimization) یا بهینهسازی فرا-اکتشافی (Meta-Heuristic) به منظور همگرایی و دستیابی به جواب بهینه سراسری یا تقریبی (Approximation) استفاده میکنند.» عملکرد محاسبات تکاملی به این شکل است که ابتدا یک مجموعه اولیه از راهحلهای کاندید (Candidate Solutions) ایجاد میکنند. در مرحله فرآیند تکاملی، الگوریتمها با دستکاری و بهروزرسانی مجموعهای متشکل از راهحلهای کاندید، مجموعه را به سمت منطقهای که حاوی راهحلهای بهینه سراسری (Global Optimum) است هدایت میکنند. هر مرحله تکرار یک نسل (Generation) نام دارد که در آن راهحلهای غیرمطلوب از مجموعه حذف شده و تغییراتی کوچک و تصادفی در راهحلهای کاندید اعمال میشوند تا فرآیند تکامل تکمیل شود. با الگوبرداری از فرآیندهای تکامل زیستی، مجموعهای متشکل از راهحلهای کاندید در تعامل با فرآیندهای تکاملی دیگر همچون جهش و انتخاب طبیعی (Natural Selection) ایجاد میشوند. در ادامه بر مبنای الگوهای تعریف شده در فرآیند تکامل، مجموعهای متشکل از راهحلهای کاندید به نحوی تکامل پیدا میکنند که با گذشت زمان برازندگی (Fitness) آنها افزایش پیدا کند (برازندگی حرکت از نسلی به نسل دیگر است). در این مرحله از تابع برازندگی (Fitness Function) برای ارزیابی و محاسبه برازندگی راهحلهای کاندید در الگوریتم تکاملی استفاده میشود. محاسبات تکاملی میتوانند مجموعهای از راهحلهای بهینه را برای یک مسئله خاص و در شرایط مختلف ایجاد کنند. رویکرد فوق درست در نقطه مقابل الگوریتمهای رایج است که تنها یک پاسخ قطعی (Deterministic Solutions) یا مجموعهای از راهحلهای تقریبی (Approximated Solutions) را برای یک مسئله ارائه میکنند. الگوریتمهای تکاملی با تولید مجموعهای از راهحلهای کاندید برای یک مسئله انتخابی مزیت بزرگی در اختیار توسعهدهندگان هوش مصنوعی قرار میدهند. تا به امروز نگارشهای مختلفی از الگوریتمهای محاسبات تکاملی ارائه شده که بیشتر آنها مستقل از دامنه و مستقل از مسئله هستند و برای پیدا کردن راهحلی برای ساختارهای دادهای خاص گزینه ایدهآلی هستند.
مفاهیم مهم مرتبط با محاسبات تکاملی
محاسبات تکاملی با هدف شبیهسازی فرآیند تکامل در یک سامانه کامپیوتری استفاده میشوند. نتیجه این رویکرد، ساخت مجموعهای از الگوریتمهای بهینهسازی است که عمدتا بر مبنای یک مجموعه ساده از ویژگیها و دستکاری آنها در یک فرآیند تکرارشونده و تکاملی به وجود میآید. در الگوریتمهای تکاملی در هر مرحله از تکرار فرآیند تکامل به شکل تدریجی و پیوسته بهبود پیدا میکند تا راهحلهای تولید شده کیفیت بهتری پیدا کنند. اینکار ادامه پیدا میکند تا یک راهحل بهینه یا تقریبی نزدیک به راهحل بهینه به دست آید. یک الگوریتم تکاملی از چهار عنصر زیر ساخته میشود:
- مولفه جمعیت: مجموعهای از نمونههای موجود در جمعیت را مدلسازی میکند.
- مولفه عملگرهای تکاملی: تغییری در کدهای ژنتیکی نمونههای موجود در جمیعت به وجود میآورد. مولفه فوق باعث ایجاد تنوع در راهحلهای کاندیدی میشود که ارائه میشوند.
- مولفه برازندگی: کیفیت راهحلهای کاندید تولید شده یا به عبارت دقیقتر همگرایی آنها با راهحل بهینه سراسری کاندید را ارزیابی میکند.
- مولفه انتخاب: سعی میکند اصل بقای برازندهترینها (Survival of the Fittest) را در الگوریتمهای تکاملی شبیهسازی کند.
انتخاب طبیعی (Natural Selection) در رویکرد تکاملی
یکی از مهمترین اصول محاسبات تکاملی، مولفه بقای برازندهترینها است. مولفه فوق با الهام گرفتن از دنیای طبیعی به الگوریتمهای تکاملی راه پیدا کرده است. در حیات وحش بقا سخت است و تنها موجوداتی قادر به بقا و تولید مثل هستند که برازندگی بیشتری داشته باشند و مابقی محکوم به فنا هستند.
یک مثال عینی در این زمینه زرافه است. گردن دراز زرافه کمک میکند تا به شاخههای بلندتری برای تغذیه دسترسی داشته باشد. به همین دلیل زرافههایی که گردن درازتری دارند، شانس بیشتری برای زندگی دارند، در این حالت هیچ عامل مستقیمی در طبیعت باعث نشده تا گردن برخی از زرافهها درازتر از سایرین شود، بلکه زرافههایی که به شکل طبیعی گردن درازتری دارند شانس بقا و تولید مثل بیشتری پیدا میکنند. متخصصان علوم کامپیوتر با الهام گرفتن از این نمونه زیستی، رویکرد انتخاب طبیعی را به منظور پیادهسازی الگوریتمهای تکاملی در سامانههای کامپیوتری ابداع کردند. اگر یک سامانه مبتنی بر محاسبات تکاملی بتواند یک جواب تقریبی برای یک مسئله بهینهسازی شده ارائه کند، با پیادهسازی تغییرات تصادفی در راهحل و ارزیابی برازندگی راهحلهای جدید، کارشناسان میتوانند تغییرات ایجاد شده را بررسی کنند و متوجه شوند کیفیت راهحلها بهبود پیدا کرده یا خیر. اگر فرآیند فوق به شکل تکرارشونده انجام شود، در هر مرحله از تکرار، دستکم یک راهحل بهتر به دست میآید. انتخاب طبیعی یکی از مولفههای کلیدی محاسبات تکاملی است که موتور محرکه آنرا عملگرهای تکاملی همچون جهش تصادفی در متغیرها شکل میدهند.
فنوتایپ و ژنوتایپ
برای درک بهتر چگونگی شبیهسازی فرآیندهای تکامل طبیعی در محاسبات تکاملی، مجبور هستیم به نقشه تکامل در زیستشناسی نگاه کنیم. در طبیعت موجودات متشکل از بدن و مجموعهای از خصلتها و رفتارها هستند. ویژگیهای یاد شده که شکل ظاهری و رفتاری یک موجود را توصیف میکنند (همچنین رنگ مو، چشم و پوست و....) فنوتایپ (Phenotype) نام دارند. شکل ظاهری تمامی موجودات زنده توسط مجموعهای از دستورالعملهای کدبندی شده در سلول آنها مشخص میشود. به این مجموعه دستورالعملهای کدگذاری شده ژنوتایپ (Genotype) میگویند.
به عبارت سادهتر، ژنوتایپ توصیفکننده اطلاعاتی است که در دیانای موجودات زنده به شکل کدگذاری شده قرار گرفته است. در محاسبات تکاملی همچون الگوریتم ژنتیک، به جمعیت راهحلهای کاندید یک مسئله بهینهسازی شده فنوتایپ میگویند. هر یک از راهحلهای کاندید، مجموعهای از ویژگیهای خاص خود را دارند که از طریق بهکارگیری عملگرهای تکاملی تغییر پیدا میکنند. به مجموعه ویژگیهای یاد شده ژنوتایپ میگویند.
آشنایی اولیه با ساختار الگوریتمهای محاسبات تکاملی
بیشتر الگوریتمهای محاسبات تکاملی بر مبنای همانندسازی الگوهای تکامل طبیعی همچون انتخاب طبیعی سعی در بهینهسازی مسائل مختلف دارند. شکل 1 ساختار کلی الگوریتمهای تکاملی را نشان میدهد. عناصر تشکیل دهنده الگوریتم فوق به شرح زیر هستند:

Initialisation (مقداردهی اولیه): برای آنکه امکان شبیهسازی فرآیندهای تکاملی در الگوریتمهای شبیهسازی فراهم شود، ابتدا باید جمعیتی از راهحلهای کاندید تولید شوند. در برخی از مسائل انتخابی نیازمند مقادیر اولیه مناسب هستیم، زیرا مقادیر اولیه متنوع دسترسی به راهحلهای بهینه متفاوتی را امکانپذیر میکنند.
Duplication (تولید مثل): در این مرحله کپیهای متعددی از راهحلهای فعلی تولید میشود.
Mutation (جهش): در این مرحله عملیات جهش روی کپیهای مختلف انجام میشود. این مرحله سعی میکند سرعت همگرایی الگوریتم به راهحل بهینه را کنترل کند.
Evaluation (ارزیابی/برازندگی): در این مرحله برازندگی هر یک از راهحلهای کاندید ارزیابی میشود تا کیفیت آنها بررسی شود. در مرحله فوق میزان همگرایی راهحلهای کاندید به راهحل بهینه سراسری مشخص میشود.
Selection (انتخاب): در این مرحله برازندگی هر یک از کپیهای ایجاد شده در جمعیت مشخص میشود تا بهترین کپی انتخاب شود و در تولید نسل بعدی از آن استفاده شود.
Output (خروجی): تکامل یک فرآیند تکرارشونده است. در این مرحله شرط توقف الگوریتم تکاملی ارزیابی میشود و اگر شرط برقرار بود بهترین راهحل کاندید ساخته شده به عنوان خروجی نشان داده میشود.
بهینه محلی (Local Maxima)
فرآیندهای تکاملی سعی میکنند برازندگی راهحلهای کاندید را افزایش داده و بهبود بخشند. در بیشتر موارد یک تابع برازندگی برای مسئله تعریف میشود. در ادامه الگوریتم سعی میکند نقطه بهینه تابع فوق را پیدا کند. در مسائلی که پیرامون مفهوم کمینه قرار دارند، هدف پیدا کردن نقطه کمینه تابع برازندگی و در مسائلی که پیرامون مفهوم بیشینه قرار دارند، هدف پیدا کردن نقطه بیشینه تابع است، اما در بیشتر موارد شکل و توزیع تابع برازندگی به وضوح مشخص نیست. به همین دلیل الگوریتم بهینهساز میتواند راهحلهای جدیدی که پیرامون نقطهای که بهترین راهحل کاندید در آن مکان پیدا شده را نمونهگیری کند. شکل 2 این موضوع را نشان میدهد. در شکل 2 مشاهده میکنید جهشهای مختلف به وجود آمده در نمونهها (محور X)، باعث به وجود آمدن امتیازات برازندگی مختلفی در محور Y شدهاند. الگوریتمهای محاسبات تکاملی با افزایش برازندگی راهحلهای کاندید، نمونههای جدیدی در همسایگی محلی (Local Neighborhood) نقطه ایکس نمونهگیری میکنند. بر مبنای اندازه همسایگی انتخاب شده، تعداد تکرارهای متفاوتی نیاز است تا الگوریتم موفق شود به نقطه بهینه سراسری همگرا دست پیدا کند.
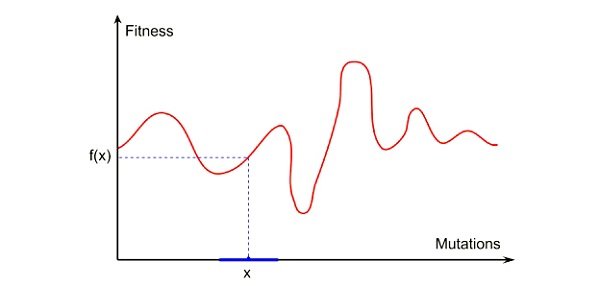
در نقطه مقابل، اگر اندازه همسایگی کوچکی انتخاب شود، الگوریتم محاسبات تکاملی با مشکل کمینه و بیشینه روبرو میشود. بهینهسازیهای محلی، راهحلهای کاندیدی هستند که بهترین راهحل در همسایگی محلی به شمار میروند و قرار نیست همواره به عنوان یک راهحل سراسری در نظر گرفته شوند. برخی از توابع بهینهکننده ممکن است شامل بهینهسازیهای محلی متعددی باشند و تنها یک راهحل بهینه سراسری داشته باشند. هر زمان الگوریتمی در دام بهینهسازی محلی گرفتار شود، این توانایی را نخواهد داشت تا راهحل بهتری برای یک مسئله پیدا کند
ماهنامه شبکه را از کجا تهیه کنیم؟
ماهنامه شبکه را میتوانید از کتابخانههای عمومی سراسر کشور و نیز از دکههای روزنامهفروشی تهیه نمائید.
ثبت اشتراک نسخه کاغذی ماهنامه شبکه
ثبت اشتراک نسخه آنلاین
کتاب الکترونیک +Network راهنمای شبکهها
- برای دانلود تنها کتاب کامل ترجمه فارسی +Network اینجا کلیک کنید.
کتاب الکترونیک دوره مقدماتی آموزش پایتون
- اگر قصد یادگیری برنامهنویسی را دارید ولی هیچ پیشزمینهای ندارید اینجا کلیک کنید.


























دیدگاهها
سلام چگونه مسئله ای داشته باشم که با استفاده از رویکردهای محاسبات تکاملی حل شده ؟ ویا با استفاده از این رویکرد قابل حل باشه