پشته چیست؟
پشته (stack) یکی از انواع ساختارهای دادهای در مبحث ساختمان دادهها است که برای ذخیره و بازیابی دادهها کاربرد دارد. پشته در طراحی و پیادهسازی سیستمهای نرمافزاری و سختافزاری، فراوان به کار میرود. شیوه عملکرد پشته بر اساس سیاست LIFO است. پشته (stack) ساختمان دادهای است که از لیست برای سازماندهی دادهها استفاده میکند و در عین حال از انتزاع نیز پشتیبانی میکند و نوعی داده انتزاعی را فراهم میکند. در پشته عمل اضافه و حذف عنصر، فقط در یک طرف آن، بهنام بالای پشته انجام میشود. یعنی عنصری که از همه دیرتر وارد پشته شد، زودتر از همه پشته حذف میشود. بههمین دلیل گفته میشود که پشته از سیاست خروج به ترتیب عکس ورود (LIFO) پیروی میکند. از آنجایی که عناصر پشته فقط از یک طرف (بالای پشته) قابل دستیابیاند. بنابراین عملیاتهای متعددی را میتوان روی پشته انجام داد که از مهمترین آنها به موارد زیر باید اشاره کرد:
Clear : تمام عناصر پشته را حذف میکند.
Push : که عنصری را به بالای پشته اضافه میکند.
Pop : که عنصر بالای پشته را حذف میکند.
Contains : مشخص میکند که عنصری در پشته وجود دارد یا خیر.
CopyTo : محتویات پشته را در آرایهای از نوع شی کپی میکند.
Peek : که عنصر بالای پشته را بازیابی میکند، اما حذف نمیکند.
StackEmpty : که خالی بودن پشته را تست میکند.
در حقیقت پشته، یکی از سه بخش تخصیص یافته به یک برنامه در حال اجرا در حافظه (RAM) است. پس از اجرای هر برنامه کاربردی آن برنامه برای پردازش توسط پردازشگر، به سه بخش در حافظه تقسیم شده و ذخیره میگردد تا در دسترس پردازشگر قرار بگیرد. این سه بخش بخش کد (شامل کد برنامه)، پشته و بخش داده (داده + بیاساس + هیپ) هستند.
FIFO و LIFO چیست؟
آخرین ورودی از همه زودتر خارج میشود LIFO سرنام Last In First Out است. این سیاست اساس کار پشتهها را تشکیل میدهد و به مفهوم آن است که آخرین داده ذخیره شده در پشته، نخستین دادهای است که بازیابی میشود. FIFO سرنام First In First Out (اولین ورودی از همه زودتر خارج میشود) است. این سیاست اساس کار صفها را تشکیل میدهد و به مفهوم آن است که اولین داده ذخیره شده در صف، نخستین دادهای نیز هست که بازیابی میشود. با توجه به آنچه گفته شد، روشن است که در سیاست LIFO، ورود و خروج دادهها، از یک سمت صورت میگیرد (در واقع تنها یک سمت توده دادهها باز است) در حالی که در سیاست FIFO، ورود و خروج دادهها، از دو سمت صورت میگیرد (یک سمت برای ورودی و یک سمت برای خروجی) و ما به دو سر تودهٔ دادهها دسترسی خواهیم داشت (یکی برای ورود و دیگری برای خروج). پیچیدگی زمانی اضافه کردن یک عنصر به یک پشته یا برداشتن یک عنصر از روی یک پشته با پیادهسازی آرایهای، از (O(1 است. این موضوع با توجه به شبهکد نمونهای که در قسمت قبل برای پیادهسازی با آرایه طرح شدهاست، کاملاً قابل توجیهاست.
میبینیم که در پیادهسازی آرایهای، پیچیدگی زمانی افزودن و برداشتن عنصرها از پشته و به پشته، با هم متفاوت است. با این وجود اگر پشته را با لیستهای پیوندی پیادهسازی کنیم، به علت ساختار خاص این لیستها، هردوی این اعمال برای پشته (و به همین شکل برای صف)، دارای پیچیدگی زمانی از (O(1 خواهد بود. پشتهها در زمینههای بسیاری به کار میروند که البته در هر زمینه کارایی مشابهی هم دارند. پشتهها برای محاسبهٔ یک عبارت ریاضی به طوری که ابتدا عملوندها و سپس عملگرها در پشته قرار میگیرند، به کار میروند. علاوه بر این، برای مدیریت حافظهٔ موردنیاز برنامه، نگهداری روند فراخوانی تابعهای مختلف در برنامه، برای پیادهسازی الگوریتم جستجوی عمق اول و… نیز از پشتهها استفاده میشود. در سیستمهایی که به شدت به پشتهها وابستهاند، علاوه بر تابعهایی که گفته شد، تابعهای دیگری نیز برای آسانتر شدن کار پیادهسازی میشوند و به این ترتیب پشتهها توسعه پیدا میکنند.
فهرست پرشی داده ساختاری
فهرست پرشی داده ساختاری احتمالاتی مبنی بر لیست پیوندی موازی است که در سال 1989 توسط William Pugh ابداع شد. در واقع فهرست پرشی یک فهرست پیوندی است که هر گره (node) آن میتواند چند گره بعد از خودش اشاره کند که تعداد آن به صورت تصادفی مشخص میشود ( هر گره در یک فهرست پیوندی از دو بخش تشکیل شده است؛ یک قسمت برای نگهداری اطلاعات و قسمت دیگر مختص اشاره گرهایی به گرههای بعدی ویا قبلی ویا هردو است .) ← به تعداد گرههایی که هر گره میتواند اشاره کند سایز گوه می گوییم.
لیست پیوندی
لیست پیوندی (Linked list) ساختاری شامل دنبالهای از عناصر است که هر عنصر دارای اشارهگری به عنصر بعدی در دنباله است. فهرست پیوندی از جمله سادهترین و رایجترین دادهساختارها است و در پیادهسازی از دادهساختارها پشته (Stack)، صف (Queue) و جدول درهمسازی (Hash table) استفاده میشود. مزیت مهم فهرست پیوندی نسبت به آرایهها این است که ترتیب قرار گرفتن دادهها در آن با ترتیب قرار گرفتن آنها در حافظه متفاوت است. به همین دلیل فهرست پیوندی دارای این ویژگی است که درج و حذف گرهها در هر نقطهای از فهرست، با تعداد ثابتی از عملیات امکانپذیر است. از طرف دیگر فهرست پیوندی اجازه دستیابی تصادفی به داده یا هرگونه اندیسگذاری را نمیدهد. در نتیجه بسیاری از اعمال ابتدایی نظیر به دست آوردن آخرین عنصر فهرست، پیدا کردن عنصر شامل داده مورد نظر، یا مشخص کردن مکان درج یک عنصر جدید ممکن است نیازمند بررسی اکثر عناصر فهرست باشد.
هر عنصر در یک فهرست پیوندی گره نامیده میشود. هر گره شامل یک فیلد کلید و یک فیلد اشارهگر است.
فهرست دایرهای و فهرست خطی
معمولاً در آخرین عنصر یک فهرست، فیلد اشاره گر اشاره گری به null است. null در زبانهای برنامهنویسی به معنای عدم وجود یک عنصر است. این نوع فهرست، فهرست خطی نامیده میشود. در نوع دیگری از فهرست پیوندی، اشاره گر عنصر آخر به عنصر اول فهرست اشاره میکند. به این نوع فهرست، فهرست پیوندی دایرهای میگویند.
فهرست دوپیوندی
در یک فهرست دوپیوندی، هرگره علاوه بر اشارهگری به عنصر بعدی دارای اشارهگری به عنصر قبلی خود نیز میباشد. در این نوع ساختمان داده هر گره یا node دو اشاره گر دارد به نامهای جلو (Front) و پشت (Back) که برای اتصال گرهها استفاده می گردد.
گره sentinel
در بعضی پیاده سازیها یک گره اضافی به نام sentinel قبل از اولین گره فهرست یا بعد از آخرین گره آن اضافه میشود. این عمل باعث سادگی و تسریع برخی از الگوریتمهای مرتبط با فهرست پیوندی میشود.
فهرست دوپیوندی در مقابل فهرست تکپیوندی
فهرست دوپیوندی به ازای هر گره به فضای بیشتری نیاز دارد و انجام عملیات اصلی بر روی آن هزینه بیشتری را صرف میکند. با این حال اداره این نوع فهرست سادهتر است. به دلیل اینکه قابلیت دسترسی ترتیبی به عناصر را در هر دو جهت دارند. به عنوان مثال، تنها با در دست داشتن آدرس یک گره میتوان با تعداد ثابتی از اعمال آن گره را از فهرست حذف یا در آن درج کرد. برای انجام همین اعمال در یک فهرست تکپیوندی آدرس گره قبل از گره مورد نظر نیز نیاز است.
فهرست دایرهای در مقابل فهرست خطی
در یک فهرست خطی اشاره گری به آخرین گره امکان دسترسی به گره اول فهرست را نیز فراهم میسازد. در نتیجه در مواردی که دسترسی به دو سر فهرست نیاز است، یک ساختار مدور تنها با یک اشاره گر امکان مدیریت کردن عناصر را فراهم میکند. سادهترین نحوه نمایش یک فهرست دایرهای خالی هنگامی است که فهرست هیچ گرهی ندارد و با یک اشاره گر به null نشان داده میشود. با توجه به این مسئله، در بسیاری از الگوریتمها باید این حالت خاص در نظر گرفته شود و بهطور جداگانه مورد بررسی قرار گیرد. در مقابل، استفاده از null برای نشان دادن یک فهرست خطی قابل درک تر است و حالتهای خاص کمتری را ایجاد میکند.
استفاده از گره sentinel
استفاده از گره sentinel باعث میشود که کاربر مطمئن شود که همه عناصر موجود در فهرست، دارای عناصر قبل و بعد هستند. به همین دلیل برخی از عملیات مربوط به فهرست سادهتر میشوند. با این حال استفاده از sentinel نیازمند فضای بیشتر است. به خصوص در برنامههایی که از تعداد زیادی فهرست کوتاه استفاده میشود. همچنین استفاده از sentinel ممکن است باعث پیچیدگی برخی اعمال شود. مانند ساختن یک فهرست خالی.
فهرست پیوندی دایرهای
در یک فهرست پیوندی دایرهای همه گرهها در یک دایره پیوسته به هم پیوند دارند. اشاره گر عنصر آخر فهرست به عنصر ابتدای آن اشاره دارد. برای داده ساختاری مانند صف، با داشتن اشاره گری به عنصر آخر فهرست، عناصر میتوانند از آخر در فهرست درج شوند و از ابتدای فهرست حذف شوند. فهرست پیوندی دایرهای میتواند تکپیوندی یا دوپیوندی باشد. هر دو نوع فهرست دایرهای قابلیت پیمایش همه عناصر فهرست، با شروع از هر یک از گرهها را دارند. این ویژگی باعث میشود که نیازی به ذخیره کردن اشاره گرهای fisrtNode و lastNode نداشته باشیم.گر چه اگر فهرست خالی باشد، به یک نمایش خاص برای نشان دادن فهرست نیاز است. در اینجا از یک متغیر lastNode استفاده شده که در صورت خالی بودن فهرست به null اشاره میکند.این نمایش باعث سادهتر شدن درج و حذف عناصر در یک فهرست غیر خالی میشود. اما یک حالت خاص برای فهرستهای خالی ایجاد میشود.
دادهساختارهای مرتبط
دادهساختارهای پشته و صف معمولاً با استفاده از فهرست پیوندی پیادهسازی میشوند.
درخت دودویی میتواند به عنوان نوعی فهرست پیوندی که هر کدام از عناصر آن خود یک فهرست پیوندی است مورد بررسی قرار گیرد. در نتیجه هر گره میتواند اشاره گری به اولین گره یک یا دو فهرست پیوندی دیگر داشته باشد که زیر درختهای آن گره را تشکیل میدهند.
فهرست پیوندی باز شده(unrolled linked list) نوعی فهرست پیوندی است که هر گره آن شامل آرایهای از دادهها است. این ساختار باعث افزایش کارایی حافظه نهان میشود. زیرا تعداد بیشتری از عناصر فهرست در حافظه پشت سر هم قرار میگیرند و سر جمع حافظه کاهش مییابد. زیرا فراداده کمتری باید برای هر عنصر فهرست ذخیره شود.
جدول در همسازی برای ساختن زنجیرهای از عناصر که در یک خانه جدول قرار میگیرند از فهرست پیوندی استفاده میکند.
صف
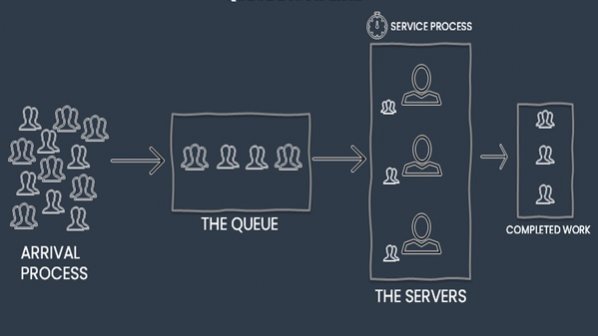
صف یکی از انواع دادهساختارهاست که از آن برای ذخیره و بازیابی دادهها بهره میبرند. صف لیستی است که عمل افزودن دادهها درون آن از انتهای لیست و عمل حذف دادهها از ابتدای لیست انجام میشود. مثل یک صف نانوایی دادهها به ترتیب ورود پشت سر هم در صف قرار میگیرند. بنابراین اولین داده ورودی اولین داده خروجی نیز خواهد بود، این به این معنی است که شیوه عملکرد صف براساس سیاست FIFO است.
صف در طراحی و پیادهسازی سیستمهای نرمافزاری و سختافزاری بسیار استفاده میشود. در این داده ساختار، دو عمل اصلی حذف کردن دادهها (Addqueue) و اضافه کردن دادهها (Delqueue) تعریف میشود.برای پیادهسازی این توابع به دو اشاره گر نیازمندیم. یکی Front که همیشه به یک عنصر قبل از عنصر ابتدایی اشاره میکند ودیگری rear که همیشه به آخرین عنصر اشاره دارد. دامنه تغییرات front و rear از 0 تا n است و مقادیر اولیه آنها 0 قرار داده میشود.شرط پر بودن صف: rear=n
صف حلقوی
ایده صف حلقوی از آنجا شکل میگیرد که اگر ما n عنصر را وارد صف کنیم و سپس آنها را یکی یکی حذف کنیم شرط پر بودن صف بر قرار میماند و این در حالی است که که صف هنوز جای خالی دارد. در صف حلقوی rear و front بعد از رسیدن به آخرین مقدار خود در صورت وجود شرایط لازم مجدداً مقادیر اولیه را میتوانند بگیرند. صف حلقوی n عضوی را به صورت آرایه 0 تا n-1 تعریف می کنیم. در این حالت وقتی rear=n-1 عنصر بعدی در [0]queue قرار میگیرد.در صف حلقوی front=rear به معنای خالی بودن صف است ولی شرط پر بودن صف بدین طریق تغییر مییابد:
صف اولویت دار
در صف عادی از تکنیک FIFO - مخفف First In First Out استفاده میشوداما در صف اولویتی برای هر داده اولویتی - نه لزوماً منحصر بفرد - مشخص میشود. صف اولویت را میتوان به اورژانس یک بیمارستان تشبیه کرد که هر بیمار با شدت بیماری بیشتر اولویت بیشتری برای رسیدگی دارد. سیستمعامل کامپیوتر هم برای مدیریت پردازشها از صفهای اولویت استفاده میکند. از ترکیب صف و پشته، دادهساختار جدیدی هم ایجاد شده که هم امکان افزودن عنصرها را از دوسوی توده دادهها میدهد و هم امکان برداشتن آنها را.
گره
گره (Node) رکوردی است که از یک فیلد داده و همچنین از یک یا چند فیلد که پیوندی به دیگر گرهها هستند، تشکیل میشود. فیلدهای داده و پیوند معمولاً توسط اشارهگرها یا مراجع پیادهسازی میشوند. هر چند که جاسازی کردن دادهها به شکل مستقیم در گره هم بسیار رایج است. گرهها برای ساختن ساختار دادههای پیوندی و سلسلهمراتبی مانند لیست پیوندی، درخت و گراف استفاده میشوند. ساختار دادههای بزرگ و پیچیدهتر میتوانند از گروهی از گرههای بهمپیوسته تشکیل شوند. از لحاظ مفهومی، گرهها مشابه راسهای تشکیلدهنده یک گراف هستند.
ماهنامه شبکه را از کجا تهیه کنیم؟
ماهنامه شبکه را میتوانید از کتابخانههای عمومی سراسر کشور و نیز از دکههای روزنامهفروشی تهیه نمائید.
ثبت اشتراک نسخه کاغذی ماهنامه شبکه
ثبت اشتراک نسخه آنلاین
کتاب الکترونیک +Network راهنمای شبکهها
- برای دانلود تنها کتاب کامل ترجمه فارسی +Network اینجا کلیک کنید.
کتاب الکترونیک دوره مقدماتی آموزش پایتون
- اگر قصد یادگیری برنامهنویسی را دارید ولی هیچ پیشزمینهای ندارید اینجا کلیک کنید.























نظر شما چیست؟